https://www.acmicpc.net/problem/1003
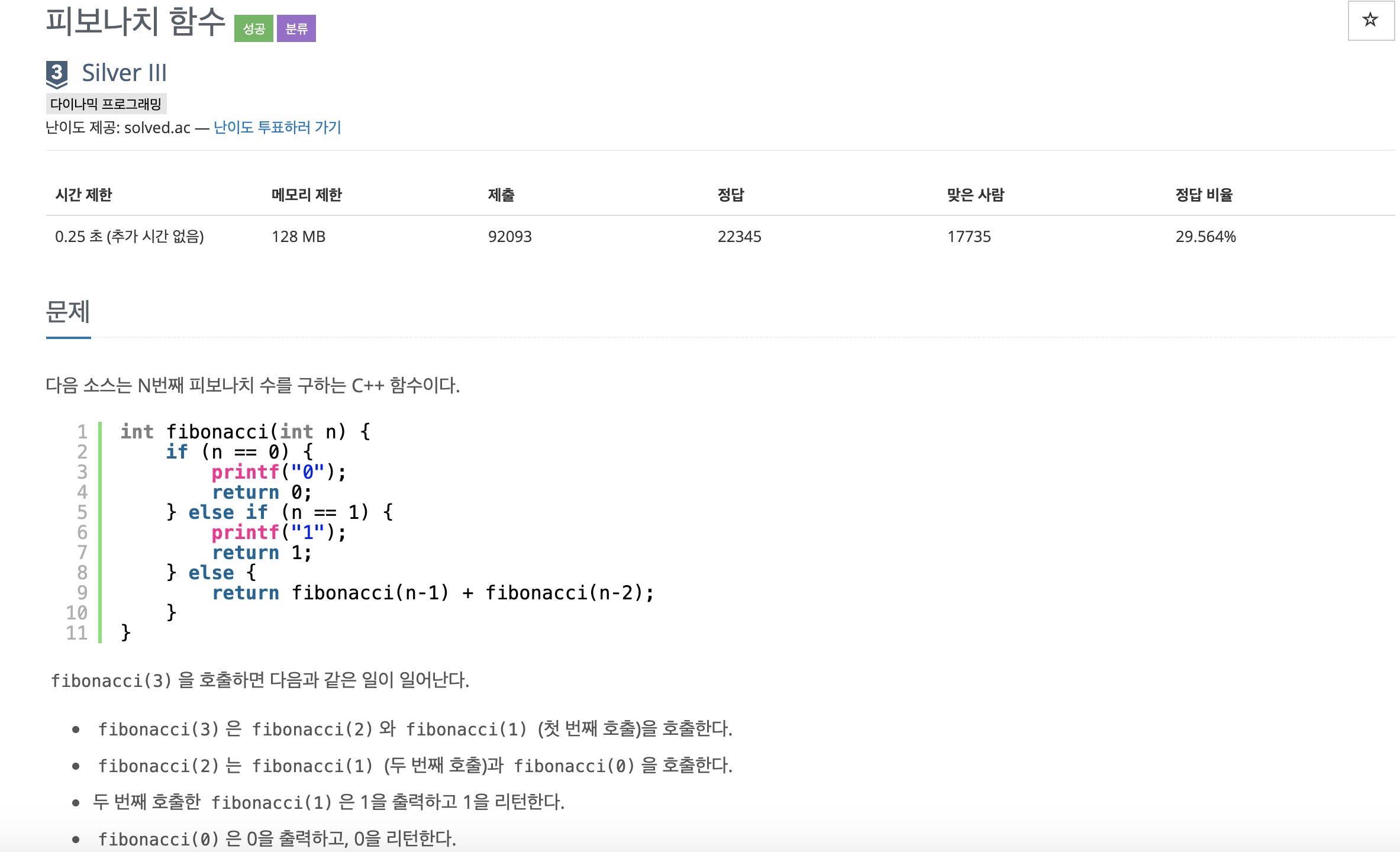
1003번: 피보나치 함수
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
www.acmicpc.net
동적계획법 C++
접근방법
피보나치 수열은 재귀로 푸는 것 보다 동적계획법으로 배열을 사용해서 푸는게
시간복잡도가 훨씬 낮다.
이는 재귀로 계산하면 계속 같은 계산을 반복해야하지만 배열에 값을 저장해두면
다음번엔 계산하지 않아도 되기 때문이다.
근데 이 문제는 이런 논리를 사용하긴하는데 수학적으로는 피보나치와 약간 연결성이 떨어져 보였다.
뭔가 푸는 방법만 같은 느낌
실제로 코드는 피보나치수열을 동적계획법으로 풀이한 것과 로직은 동일하다.
어렵게 생각하지 말고 그냥 트리나 표를 그려서 접근하는게 좋을 것 같다.
시간제한이 0.25초라 겁먹었는데 맞았습니다 나와서 놀란 문제..
소스코드
#include <iostream>
using namespace std;
int fibo[40][2];
int main(){
fibo[0][0] = 1;
fibo[0][1] = 0;
fibo[1][0] = 0;
fibo[1][1] = 1;
int c,n;
cin >> c;
for(int i = 0 ; i < c ; i++){
cin >> n;
if(n <= 1){
cout << fibo[n][0] << " "<<fibo[n][1] << "\n";
continue;
}
for(int i = 2 ; i <= n; i++){
fibo[i][0] = fibo[i-1][0] + fibo[i-2][0];
fibo[i][1] = fibo[i-1][1] + fibo[i-2][1];
}
cout << fibo[n][0] << " " << fibo[n][1] << "\n";
}
return 0;
}728x90
'알고리즘 문제풀이' 카테고리의 다른 글
| [백준 9461] 알고리즘 26일차 : 파도반 수열 (0) | 2020.07.20 |
|---|---|
| [백준 1904] 알고리즘 25일차 : 01타일 (0) | 2020.07.18 |
| [백준 1676] 알고리즘 23일차 : 팩토리얼 0의 개수 (0) | 2020.07.15 |
| [백준 11653] 알고리즘 22일차 : 소인수분해 (0) | 2020.07.14 |
| [백준 1037] 알고리즘 21일차 : 약수 (0) | 2020.07.13 |


