https://www.acmicpc.net/problem/12865
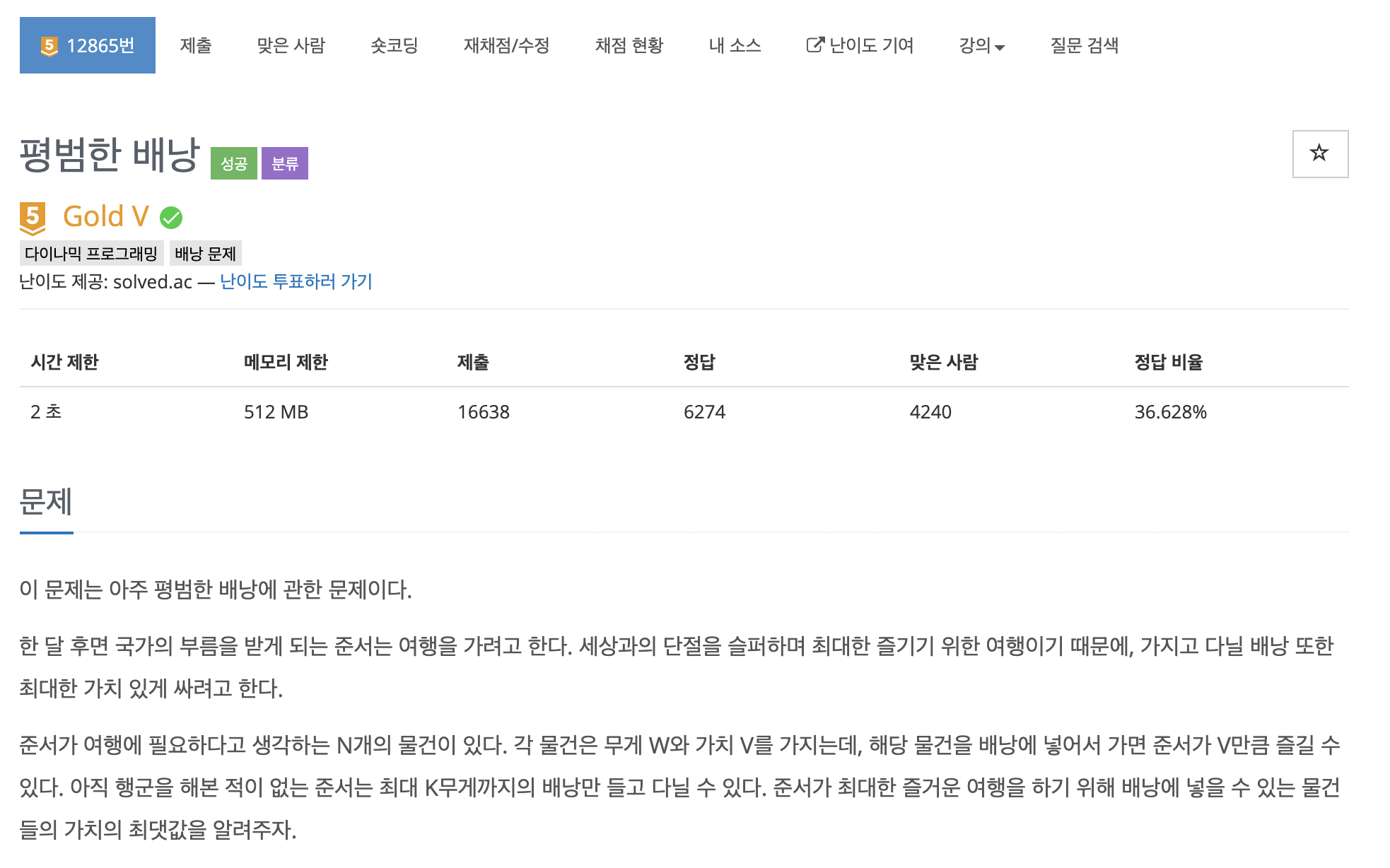
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
동적계획법 C++
2020 하계 방학 알고리즘 스터디의 마지막을 장식할 DP 문제 knapsack 문제다!!!
문제는 설명하기 입아프니 위 사진을 참고하도록 하시고
이번 여름방학 스터디 마지막 문제로 knapsack 문제를 정석으로 코드를 짜보려고
이 문제를 골랐다.
접근방법
상향식 접근, 최적의 원리 등의 접근으로 풀이하는 대표적인 DP문제 중 하나인 knapsack(배낭채우기 0-1)문제
0-1이 아니면 그리디로 풀이하면 되지만 0-1은 DP로 풀이해야한다.
하지만 knapsack을 DP로 풀이한 아래 풀이법은 시간복잡도가 O(NW)이다.
배낭에 담을 수 있는 무게가 너무 커지면 이것도 N^2이상의 복잡도를 갖는다. (NP문제)
갖고있는 물건의 개수 만큼의 행을 갖고, 배낭에 담을 수 있는 무게의 범위 만큼의 열을 갖는 이차원 배열을 사용한다.
배열에 저장되는 값은 이렇다. (행 : i, 열 : w) i까지의 물건을 w무게 만큼 넣을 수 있다고 할때 가장 큰 가치를 저장한다.
이때 i번째 물건을 넣지 않았을 때와 i번째 물건을 넣을 공간을 마련한 후 i번째 물건을 넣었을 때의 배낭에 든 물건의 가치를 비교한다.
이때 추가로 처리하는 것은 w무게 보다 i번째 물건의 무게가 클때 이때는 i번째 물건을 넣지 않았을 때의 경우와 같은 값을 저장한다.
소스코드
#include <iostream>
using namespace std;
int dp[101][100001];
int main(){
int n, k;
cin >> n >> k;
int weight, worth;
for(int i = 1 ; i <= n ; i++){
cin >> weight >> worth;
for(int w = 0 ; w <= k ; w++){
if(weight > w || (worth+dp[i-1][w-weight] < dp[i-1][w]) )
dp[i][w] = dp[i-1][w];
else
dp[i][w] = dp[i-1][w-weight] + worth;
}
}
cout << dp[n][k];
return 0;
}
가독성을 지닌 2024버전 평범한 배낭
#include <iostream>
#include <vector>
using namespace std;
int main(){
int n, capacity;
cin >> n >> capacity;
vector<vector<int>> knapsack(n+1, vector<int>(capacity+1, 0));
for(int item = 1 ; item <= n ; item++){
int weight, value;
cin >> weight >> value;
for(int cur_cap = 1 ; cur_cap <= capacity ; cur_cap++){
int total_value_without_item = knapsack[item-1][cur_cap];
int total_value_with_item = knapsack[item-1][cur_cap - weight] + value;
if(cur_cap < weight || total_value_with_item < total_value_without_item){
// 배낭에 item 넣지 않음
knapsack[item][cur_cap] = knapsack[item-1][cur_cap];
}else{
// 배낭에 item 넣음
knapsack[item][cur_cap] = total_value_with_item;
}
}
}
cout << knapsack[n][capacity];
return 0;
}
Swift 풀이 (헷갈렸던거 정리)
- 스위프트로 입력 받는 거 여전히 익숙하지 않아서 찾아보면서 함
- 2차원 배열 사이즈 지정, 기본값 지정
- range (a...b이면 a <= i <= b, a..<b 이면 a <= i < b)
- if 조건문은 괄호 유무 상관 X, for 문 범위 부분은 괄호 X
import Foundation
let inputs = readLine()?.split(separator: " ")
let n:Int = Int(inputs![0])!
let cap:Int = Int(inputs![1])!
var arr: [[Int]] = Array(repeating: Array(repeating: 0, count: cap+1), count: n+1)
var weight = 0
var value = 0
for i in 1...n {
let input = readLine()?.split(separator: " ")
weight = Int(input![0])!
value = Int(input![1])!
for j in 1...cap {
if j < weight || arr[i-1][j] > arr[i-1][j-weight]+value {
arr[i][j] = arr[i-1][j]
} else {
arr[i][j] = arr[i-1][j-weight]+value
}
}
}
print(arr[n][cap])
이건 2025.04.01 풀이
위 코드 보다 조금 더 비효율적이긴 한데, 가독성은 훨씬 좋을 듯.
입력받을 때 마다 처리하는 것에서 inven(tory)에 아이템들을 담고 처리하는 방식
import Foundation
struct Item {
let weight:Int
let value:Int
}
func solution() -> Int {
let nk:[Int] = (readLine()?.split(separator: " ").map { Int($0)! })!
let (n, k) = (nk[0], nk[1])
var dp:[[Int]] = [[Int]](repeating: [Int](repeating: 0, count: n+1), count: k+1)
var inven:[Item] = [Item(weight: 0, value: 0)]
for _ in 0..<n {
let wv:[Int] = (readLine()?.split(separator: " ").map { Int($0)! })!
inven.append(Item(weight: wv[0], value: wv[1]))
}
for wlimit in 1...k {
for ci in 1...n {
let itemWeight = inven[ci].weight
let itemValue = inven[ci].value
if wlimit >= itemWeight {
let maxValueWithMe: Int = dp[wlimit-itemWeight][ci-1] + itemValue
dp[wlimit][ci] = maxValueWithMe
}
let maxValueWithoutMe: Int = dp[wlimit][ci-1]
dp[wlimit][ci] = max(dp[wlimit][ci], maxValueWithoutMe)
}
}
return dp[k][n]
}
print(solution())'알고리즘 문제풀이' 카테고리의 다른 글
| [백준 1654]알고리즘 55일차 : 랜선 자르기 (0) | 2020.12.29 |
|---|---|
| [백준 10816] 알고리즘 54일차 : 숫자 카드 2 (0) | 2020.12.28 |
| [백준 11057] 알고리즘 52일차 : 오르막 수 (0) | 2020.08.27 |
| [백준 11054] 알고리즘 51일차 : 가장 긴 바이토닉 부분 수열 (0) | 2020.08.26 |
| [백준 9095] 알고리즘 50일차 : 1,2,3더하기 (0) | 2020.08.25 |



